Dieser Artikel erklärt Fehlerquellen und deren Größenordnung bei der Deviationsmessung mittels GPS und zeigt Möglichkeiten zur Fehlerkorrektur.

Was bisher besprochen wurde

In den ersten drei Teilen wurden die Grundlagen von (Magnet-)Kompassen und Magnetfeldern diskutiert. Es wurde die Ursache für die Deviation erklärt, sowie eine Methode zur Erstellung einer eigenen Deviationstabelle mittels GPS vorgestellt. Auch der zur erwartende Positionsfehler (Besteckversetzung) ohne Deviationskorrektur wurde gezeigt: Bei einem Kursfehler von 5° liegt die Besteckversetzung nach 12 Seemeilen bei 1 Seemeile. Die Deviationsmessung auf vielen verschiedenen Jachten im Laufe der Jahre hat gezeigt, dass Abweichen von ± 10° durchaus normal sind, teilweise sogar höher. Umso wichtiger ist es, eine genau Tabelle zu erstellen. 

Genauigkeit der GPS-Deviationsmessung

Die Genauigkeit der Deviationstabelle, d.h. die Größe der Messfehler, hängt von mehreren Faktoren ab.

Nochmals kurz zusammengefasst beruht die in Teil 3 vorgestellte Messmethode auf einem Vergleich des Magnetkompasskurses durchs Wasser mit dem mittels GPS ermitteltem rechtweisenden Kurs über Grund (COG). Beide Kurse sind mit einem Fehler behaftet. Idealerweise liegen beide Kurse exakt übereinander, dann besteht die Differenz der abgelesenen Werte ausschließlich aus den magnetischen Komponenten Deviation und Variation.

Decken sich beide Kurse nicht, so summieren sich die Fehler und die Deviationstabelle wird ungenauer. Es lassen sich die Fehler nachträglich kaum rechnerisch entfernen. Deshalb ist es wichtig, Messfehler von vornherein zu vermeiden.

Genauigkeit des COG

Messfehler im COG können durch folgende Ursachen entstehen:

• Konfiguration des GPS-Gerätes.
• Messgenauigkeit des GPS.
• Abdrift durch Wind.
• Strömung.

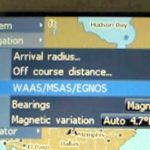
Konfiguration des GPS-Gerätes

Manche Plotter zeigen den magnetischen Kurs (M) an, der von der Software um die Variation korrigiert wird. Da in der Berechnung der Deviationstabelle diese ebenfalls berücksichtigt wird, würde sie somit doppelt einfließen. Das wiederum würde zu einer linearen Verschiebung der Kurve in y-Richtung führen.

Konfiguration der Variation.

In den meisten GPS-Geräten kann man in den Einstellungen festlegen, ob man den magnetischen (magnetic) oder den rechtweisenden (wahren) Kurs (true) sehen möchte und kann die Variation (magnetic variation) einstellen. Man hat die Wahl zwischen „automatic“ und „manual“. Es ist empfohlen das Handbuch zu befragen, um sicher zu sein, welchen Wert das Geräte anzeigt, bzw. wie man es richtig konfiguriert. Um sicher zu gehen, kann man während der Erstellung der Deviationstabelle auf „manual, 0°“ stellen.

Messgenauigkeit des GPS-Gerätes

Ein weiterer Fehler kann durch die prinzipielle Messungenauigkeit des GPS entstehen. Auf See hat man i.d.R. einen sehr guten Satellitenempfang, trotzdem liegt die maximale Messgenauigkeit „nur“ zwischen 2 und 5 Metern. Das ist prinzipiell zwar viel genauer, als man für eine Positionsbestimmung auf einem Schiff benötigen würde, allerdings nicht für die Kursberechnung.

Theoretischer COG-Fehlerwinkel.

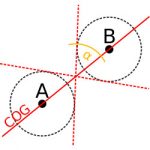
Ein GPS-Gerät ermittelt in regelmäßigen Zeitabständen mittels Satelliten die aktuelle Position. der Kurs wird aus zwei aufeinander folgenden Positionen errechnet. Die Abbildung rechts zeigt zwei Positionen A und B und den errechneten COG. Aufgrund der Messgenauigkeit liegt der tatsächliche Ort allerdings irgendwie innerhalb der strichlierten schwarzen Kreise und nicht unbedingt genau im Mittelpunkt. Die beiden roten Tangenten sind somit auch gültige Ergebnisse für den COG. In dieser Grafik ergibt das ein Fehlerwinkel α, d.h. eine Schwankungsbreite von ca. ± 50°.

Nimmt man an, dass sich das Boot mit 6 Knoten bewegt, sind das umgerechnet ca. 3 Meter pro Sekunde. Nimmt man weiter an, dass das GPS-Gerät einmal pro Sekunde eine Position mit einer Messgenauigkeit von 3 Metern berechnet, ist ganz offensichtlich, dass die Entfernung zwischen den beiden Punkten gleich groß ist, wie die Positionsgenauigkeit. Der maximale Schwankungsbreite des errechneten Kurses ist dann sogar noch viel größer, als in obiger Grafik dargestellt.

Das erklärt auch, warum die Kursanzeige auf einem GPS-Gerät nie stabil einen Wert anzeigt, sondern immer um einige Stellen springt. Der tatsächliche Anzeigefehler wird in der Praxis aber nicht, wie oben gezeigt bei 50° oder mehr liegen, sondern wird wesentlich kleiner sein. In der Software werden intelligente Algorithmen implementiert (z.B. Kalman-Filter), die das kompensieren.[1. Man kann nämlich annehmen, dass ein Schiff nicht innerhalb einer Sekunde seinen Kurs um 50° ändern kann.]

Es lässt sich einfach herleiten, dass man den Fehlerwinkel folgendermaßen berechnen kann:

… GPS-Fehler.
… Entfernung zwischen den beiden Messungen.

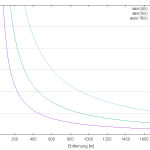
Beträgt die GPS-Genauigkeit 2 Meter und Abstand zwischen den Positionsbestimmungen 3 Meter, so beträgt der Winkelfehler ±42°.

Abhängigkeit Fehlerwinkel zur Distanz.

Damit lässt sich umgekehrt auch feststellen, dass  bei einer GPS-Genauigkeit von 4 Metern der Fehlerwinkel nach 1,2 Kabellängen (229 Meter) nur mehr ±1°, und nach 2,5 Kabellängen (458 Meter) nur mehr ±0,5° beträgt. Bei einer GPS-Genauigkeit von nur 8 Metern fällt der Fehlerwinkel nach 2,5 Kabellänger unter ±1° und nach 0,5 Seemeilen unter ±0,5°. Die Abbildung rechts zeigt, wie der Fehlerwinkel mit zunehmender Entfernung immer kleiner wird, in Abhängigkeit der GPS-Genauigkeit (violett 4 m, grün 8 m, blau 16 m). Bei 6 Knoten Geschwindigkeit entsprechen 2,5 Kabellängen 2,5 Minuten Fahrzeit.

Um die COG-Messung und somit die Genauigkeit der Deviationstabelle zu verbessern, kann man anstatt der einfachen Mittelwertschätzung der COG-Anzeige folgendermaßen vorgehen: Den gegebenen Kompasskurs am einfachsten unter Zuhilfenahme des Autopiloten exakt steuern. Sobald das Boot stabil auf Kurs ist am GPS einen Wegpunkt setzen und den Kurs ca. 2 Minuten beibehalten. Nach Ablauf der Zeit einen weiteren Wegpunkt setzen und die (rechtweisende) Peilung am Plotter zwischen dem ersten und dem zweiten Wegpunkt ermitteln.[1. Anstatt des zweiten Wegpunktes könnte man auch die Peilung von der aktuelle Position zurück zum ersten Wegpunkt ermitteln und 180° addieren.]

Abdrift durch Wind

Die seitliche Abdrift durch den Wind spielt eine wesentliche Rolle. Diese Fehlerquelle lässt sich aber sehr einfach erkennen und somit auch eliminieren. Idealerweise führt man die Messung bei Windstille und glatter See durch. Bei mehr als 2 Bft sollte man das Ganze auf einen anderen Zeitpunkt verschieben. Der Wellengang ermöglicht auch kein exaktes Steuern.

Messfehler durch Strömung

Wesentlich schwieriger als der Wind ist die Strömung zu beurteilen. Ist die Strömung so stark, dass man sie mit freiem Auge sieht, sollte man von der Erstellung einer Deviationstabelle Abstand nehmen.

Die Auswirkung der Strömung auf den COG ist sehr hoch. Nimmt man einen Strom von 2 Knoten an, zu dem man genau quer mit 6 Knoten fährt, ergibt sich ein Fehlerwinkel von ungefähr und bei einem Strom von nur 0,3 Knoten liegt der Fehlerwinkeln noch bei 2,9°.

Für die exakte Berechnung wird der Kosinussatz herangezogen, da sich aus der Beziehung des Kurses zum Strom ein allgemeines Dreieck in Abhängigkeit der Geschwindigkeiten ergibt. Die Formeln sind hier zur Vollständigkeit angegeben, gearbeitet werden kann aber mit der Strömungskurve (s. unten).

Strömungsfehlerkurve.

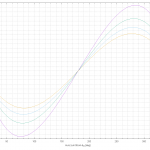
Die Abbildung[1. Die Kurve wurde mit GNUplot erstellt. Hier der vollständige Source-Code.] rechts zeigt den Fehlerwinkel bei einem Strom von 1 Knoten und verschiedenen Bootsgeschwindigkeiten. Auf der X-Achse ist der Kurs relativ zum Strom aufgetragen. Die Kurven können mit der tatsächlichen Stromgeschwindigkeit multipliziert werden, um den entsprechenden Fehlerwinkel zu erhalten.[1. Dieselbe Berechnung bzw. dieselbe Kurve könnte auch zur Stromnavigation herangezogen werden, die normalerweise geometrisch konstruiert wird.]

Anwendung der Strömungsfehlerkurve

Beispiel: Der Strom setzt nach 330° mit 0,3 Knoten, bei einer Bootsgeschwindigkeit von 6 Knoten bei einem Kompasskurs von 270°. Alle anderen Beschickungen (Variation, etc.) werden mit 0 angenommen. Wie groß ist der Fehlerwinkel? Wie groß ist der COG?

Zuerst den Kurs relativ zum Strom berechnen:

Nun den Fehlerwinkel aus der Tabelle bei 300° auf der blauen 6-Knoten-Kurven ablesen -> +9°. Weil der Strom aber 0,3 Knoten beträgt gerundet daher +3°. Der COG beträgt daher .

Nimmt man nun an, dass man bei diesen Gegebenheiten eine Deviationstabelle erstellt, ohne den Strom mit einzubeziehen, wäre die Deviation bei 270 um +3° zu hoch. Infolgedessen muss der aus obiger Tabelle ermittelte Strömungsfehlerwinkel in der Deviationstabelle negativ berücksichtigt werden.

Ermittlung der Strömung

Ist der Strom bekannt, lässt sich mit obiger Methode eine sehr passable Berichtigung der Deviationsmessung durchführen. Die Feststellung des Stromes ist aber nicht besonders einfach.

Voraussetzung ist wieder einmal möglichst Windstille. Die Yacht abstoppen und einen Wegpunkt mit dem GPS setzen. Eine halbe Stunde warten, danach mit dem GPS die Entfernung und den Winkel von der aktuellen Position zum zuvor gesetzten Wegpunkt ermitteln. Stromgeschwindigkeit ist die Entfernung multipliziert mit 2 (wegen der halben Stunde) und die Stromrichtung ist die Peilung zum Wegpunkt + 180.

Um festzustellen, ob es sich um einen konstanten Meeresstrom oder einen Gezeitenstrom handelt, sollte man die Strömungsermittlung unmittelbar nach Erstellung der Deviationstabelle wiederholen. Sofern sich die Strömungswerte der ersten und zweiten Messung nicht zu sehr unterscheiden, kann man den Mittelwert bilden und damit die Deviationstabelle korrigieren.

Kompensation eines Gezeitenstroms

Sollte es sich um einen Gezeitenstrom handeln, kann man diesen Kompensieren, indem man zwei Deviationsmessungen im Abstand von ca. 6¼ Stunden durchführt. Das ist die mittlere Zeit, nach der der Gezeitenstrom kippt. Nimmt man die Mittelwerte der Deviationen aus der ersten und der zweiten Messung, hebt sich dadurch der Strömungsfehler auf. Das stimmt natürlich nur dann, wenn Ebbe und Flut die gleiche Strömungsgeschwindigkeit und Richtung (+180°) haben, wobei in erster Linie die Geschwindigkeit entscheidend ist.

Genauigkeit des Magnetkompasskurses

Die Genauigkeit des Magnetkompasskurses hängt von der Genauigkeit der Skala, vom Seegang und vom Rudergänger bzw. vom Autopilot, und von etwaigen zusätzlichen Magnetfeldern ab. Auf letzteres sollte besonders geachtet werden, d.h. sämtliche ferromagnetischen oder anderen magnetfelderzeugenden Gegenstände vom Kompass entfernen (Winschkurbel, Taschenlampen, Mobiltelefone, Lifelines,…).

Auf den wenigsten Kompassen ist die Skala auf 1° geteilt, sondern meistens nur 5°, man kann erfahrungsgemäß aber trotzdem bis auf 1° schätzen. Schwieriger wird die Messung bei Seegang, weil der Kompass dann schwankt und man doch den Kurs für einige Zeit stabil halten sollte, weshalb die Erstellung der Deviationstabelle nach dem GPS-Verfahren auch nicht vernünftig möglich ist.

Der Magnetkompass sollte eigentlich exakt parallel zur Mittschiffslinie ausgerichtet sein. Genau umgekehrt als beim GPS ergibt sich der Kompasskurs nicht aus der Bewegung, sondern direkt aus der Stellung des Schiffes zum Magnetfeld. Die Schiffsbewegung spielt dabei keine Rolle. Wenn der Bug nach Norden zeigt, misst der Kompass 0°, auch wenn man das Schiff quer durchs Wasser schieben würde.

In Teil 3 dieser Artikelreihe wurde die Deviationstabelle der Segelyacht Demi gezeigt. Die Kurve ist um ca. 3° nach unten verschoben. Die Ursache für ein solche lineare Verschiebung entlang der Y-Achse rührt daher, dass entweder der Kompass nicht exakt parallel zur Mittschiffslinie montiert wurde, oder dass das Schiff nicht wirklich genau parallel durchs Wasser fährt. Dieser Fehler ist für die Deviationstabelle aber irrelevant, da er immer gleich auftritt und somit nicht kompensiert werden muss.

Fazit

In diesem Artikel wurden verschieden Fehlerquellen, die sich auf das GPS-Verfahren zur Erstellung der Deviationstabelle beziehen, diskutiert. Es wurden deren Größenordnung und Kompensationsmethoden vorgestellt.

Es wurde gezeigt, dass eine Strömung das Ergebnis maßgeblich beeinflusst und daher unbedingt berücksichtigt werden muss.

Fortsetzung folgt

Im folgenden Artikel werden andere Methoden zur Deviationsmessung vorgestellt. Es wird auch eine Software präsentiert, die im Rahmen dieser Arbeiten mit Deviationstabellen entstanden ist. Das Programm kann zu Erstellung von Deviationskurven nach erfolgter Messung verwendet werden.